Со времен досократиков фундаментальной проблемой философии природы было установление того, каким образом из сложных, нерегулярных и хаотичных состояний материи возникает порядок [2.1]. Фи-лософы-досократики рассматривали сложность непосредственно наблюдаемых природных явлений как данное и старались свести ее к «первоосновам» (ар)(1Г)), «принципам» или определенному порядку. Приведем несколько примеров. Фалес из Милета (625-545 гг. до н. э.), про которого говорят, что он доказал первые геометрические теоремы, был также первым натурофилософом, считавшим, что исходными причинами всех вещей могут быть только материальные первопричины. В качестве начала всего Фалес положил воду или влагу. Его аргументы основаны на наблюдении, что пища и семя всех существ влажные, а естественной средой влажных вещей является вода.
Со времен досократиков фундаментальной проблемой философии природы было установление того, каким образом из сложных, нерегулярных и хаотичных состояний материи возникает порядок [2.1]. Фи-лософы-досократики рассматривали сложность непосредственно наблюдаемых природных явлений как данное и старались свести ее к «первоосновам» (ар)(1Г)), «принципам» или определенному порядку. Приведем несколько примеров. Фалес из Милета (625-545 гг. до н. э.), про которого говорят, что он доказал первые геометрические теоремы, был также первым натурофилософом, считавшим, что исходными причинами всех вещей могут быть только материальные первопричины. В качестве начала всего Фалес положил воду или влагу. Его аргументы основаны на наблюдении, что пища и семя всех существ влажные, а естественной средой влажных вещей является вода.Анаксимандр (610-545 гг. до н. э.), который считается учеником и последователем Фалеса, расширил его философию природы. Почему именно вода должна быть первопричиной всего сущего? Она есть лишь одна из многих форм материи, которые существуют в непрерывных взаимных напряжениях и борьбе противоположностей: теплота против огня, влага против сухости... Поэтому Анаксимандр предполагает, что «начало и первопричина всех существующих вещей» — это «безграничная неопределимая» первичная материя апейрон (omeipov), из которой возникли противоположные формы материи. Соответственно мы должны представлять себе «безгранично неопределимое» как первичное состояние, в котором материя была безгранична, не имела противоположностей и поэтому везде была однотипной. Следовательно, это было начальное состояние, обладающее однородностью и совершенной симметрией. Затем происходит нарушение симметрии, благодаря чему возникает мир со всеми наблюдаемыми противоположностями и напряжениями:
...При зарождении этого мира из вечного выделилось животворное начало теплого и холодного, и некая сфера из этого пламени облекла окружающий землю воздух, как кора — дерево. А когда она разорвалась и замкнулась в кольца, возникли солнце, луна и звезды [2.2] Поэтому последующие состояния материи, которые описывает Анаксимандр в своей космогонии, совершенно не были хаотическими, напротив, они определялись новыми видами упорядоченности. Восхищение Анаксимандром возрастает еще больше, когда мы знакомимся с его ранними идеями о биологической эволюции. Он предполагает, что первые человеческие существа были рождены морскими животными, молодь которых быстро приспособилась поддерживать друг друга, как это он наблюдал у определенного вида акул. Всего столетием спустя уже проводились поиски останков морских животных как свидетельства того, что люди возникли из моря.
Третьим знаменитым милетским философом природы был Анаксимен (около 525 г. до н. э.), который считается последователем Анаксимандра. Анаксимен рассматривает изменение как явление, обусловленное внешними силами сгущения и разрежения.
По его мнению, каждая форма материи может считаться основной. Сам он выбирает за основу воздух (агра):
...При разрежении рождается огонь, а при сгущении — ветер, затем туман, вода, земля, камень. А из этого возникает все прочее. Движение же Анаксимен считает вечным. Благодаря ему все вещи превращаются друг в друга. Он говорит, что холод сжимает и сгущает вещи; напротив, теплота расширяет и разжижает их [2.3].
Таким образом, Анаксимен предполагает, что существуют внешние силы, создающие из единой первичной материи различные преобразующиеся друг в друга состояния.
Взгляды Гераклита из Эфеса (около 500 г. до н.э.), которого часто называли «темным», имеют очень большое значение для нашей темы. Конечно, язык Гераклита загадочен, он больше пророческий, чем рассудочно научный, и полон проницательных метафор. Он взял от Анаксимандра учение о борьбе и столкновении противоположностей в природе. Первичная материя — источник всего — сама есть изменение, и поэтому отождествляется с огнем:
...Всем управляет молния. Этот космос, тот же самый для всех, не создал никто ни из богов, ни из людей, но он всегда был, есть и будет вечно живым огнем, мерами разгорающимся и мерами погасающим [2.4].
Далее Гераклит разрабатывает учение о том, каким образом все состояния материи можно рассматривать как различные формы первичной материи — огня. В наши дни физик Вернер Гейзенберг утверждал:
...Здесь можно заметить, что в определенном смысле современная физика чрезвычайно сильно сближается с учением Гераклита. Если заменить
слово «огонь», то можно увидеть, что утверждения Гераклита почти слово в слово совпадают с современными представлениями. Энергия действительно является тем материалом, из которого сделаны все элементарные частицы, все атомы и поэтому вообще все вещи, и в то же время энергия — это то, что движется... Энергия может превращаться в движение, теплоту, свет и давление. Энергию можно рассматривать как причину всех изменений, происходящих в мире [2.5].
Мы видим, что в материальном мире властвуют противоположные условия и тенденции, которые, тем не менее, объединены скрытой гармонией: «Противоречивость сближает, разнообразие порождает прекраснейшую гармонию (apuov.oc), и все через распрю создается» [2.6]. Таким образом, скрытая гармония противоположностей есть космический закон Гераклита, который был им назван «логосом» (Хоуос;).
Что происходит, когда борьба противоположностей заканчивается? Согласно Гераклиту, тогда мир приходит к конечному состоянию абсолютного равновесия. Парменид Элейский (около 500 г. до п. э.) описал состояние материи, в котором не происходит никаких изменений и движений в (пустом) пространстве. В этом случае материя распределена везде равномерно (однородно) и так, что отсутствует выделенное направление возможного движения (изотропно). Примечательно, что бесконечность рассматривается как недостаток, поэтому предполагается, что распределение материи конечно. Рассуждая подобным образом, Парменид приходит к образу мира, представляющему собой твердый, конечный, однородный материальный шар вне времени, без движения и изменения. Элеатская философия неизменного бытия была на самом деле направлена против ге-раклитовской философии непрерывного изменения, которая отвергалась как всего лишь иллюзия чувств. Позднейшее историческое влияние элеат-ской философии на философию Платона ощущается в его критике вводящих в заблуждение изменений, связанных с чувственным восприятием, в противоположность истинному миру неизменного существования идей. Однако, с точки зрения философии природы, мир, описанный Пармени-дом, не обязательно противоречит учению Гераклита; в его космогонии мир Парменида можно вполне понимать как сингулярное конечное состояние с наивысшей симметрией.
После того как вода, воздух и огонь были признаны первичными элементами, было легко представить себе эти элементы как сырье для построения мира. Этот шаг сделал Эм-педокл (492-430 гг. до н.э.), добавив к огню, воде и воздуху четвертый элемент, землю. Эти элементы могут свободно перемешиваться и соединяться в любых пропорциях, а также могут растворяться и разделяться. Каковы же, согласно Эмпедоклу, те неизменные принципы, которые лежат в основе постоянных изменений и движений в природе? Во-первых, это четыре элемента, которые, как полагал философ, возникают из природы и случая (tu/e), а не в результате сознательного намерения. Изменения вызваны обратным влиянием этих элементов друг на друга, т. е. их смешиванием и разделением:
Хочу сказать вам еще одно. Элементы эти всегда пребывают, они не рождаются и не завершают свой путь разрушительной смертью. Есть только одно: смешивание и обмен тем, что смешалось [2.7].
За эти взаимно обратные явления ответственны две основные энергии. Эмпедокл назвал их «любовью» (rpiXia) для притяжения и «враждой» (veixoc) для отталкивания. Здесь видна аналогия с дуализмом инь — ян в китайской философии. Эмпедокл говорил о постоянном процессе изменений, т. е. о соединении и разделении элементов, при которых сами элементы сохраняются. Он считал, что все процессы изменений являются не механическими (как позднее полагали атомисты), а, скорее, физиологическими, тем самым перенося процессы метаболизма в организмах на неживую материю.
В медицине, по Эмпедоклу, равновесие понимается как особенно гармоничная связь. Таким образом, здоровье означает индивидуальный баланс противоположных компонентов, а болезнь возникает тогда, когда один из компонентов берет верх. Если вспомнить современную бактериологию с ее знанием о существовании антител в человеческом организме, то этот взгляд Эмпедокла покажется удивительно современным.
Анаксагор (499-426 гг. до н. э.) развивал взгляды, во многом представлявшие усовершенствование учений его предшественников. Вслед за Эмпедоклом он разрабатывал теорию смешивания материи. Но Анаксагор заменил четыре элемента Эмпедокла неограниченным числом субстанций, состоящих из семян (апериата) или частиц одинаковых размеров (rjfioio-[lEprj (аоцата)). Число этих частиц и степень их малости ничем не ограничены, т. е. предполагается, что материя бесконечно делима. На ум неизбежно приходит идея зернистого континуума. Анаксагор пытался таким образом объяснить и смешивание цветов, говоря, что снег в определенной степени черный, хотя белизна в нем доминирует. Во всем заключается часть всего, и существуют лишь различия в пропорциях смешивания.
Анаксагор попытался в своей философии природы дать более отчетливые, чем ряд его предшественников, физические объяснения небесным явлениям и движениям, которые в математической астрономии греков описывались лишь кинематически. Так, в своей космологии он исходил из сингулярного начального состояния, представляющего однородную смесь материи. Нематериальное первоначало, названное Анаксагором «умом» «нус» (vout;), приводит эту смесь в круговое движение, которое производит отделение различных вещей, в зависимости от скорости каждой из них. Земля держится в середине вихря, а более тяжелые куски камней выбрасываются наружу и образуют звезды. Их свет объясняется свечением их масс, обусловленным большой скоростью вращения. Теория вихрей Анаксагора вновь возникла в наше время у Декарта и в более усовершенсnвовнной форме в теории механического происхождения планетных систем Канта—Лапласа.
В современном естествознании атомизм оказался чрезвычайно успешной исследовательской программой. В истории философии атомную теорию Демокрита часто излагают как следствие философии изменчивости Гераклита и принципа неизменного бытия Парменида. Демокритовское различие между «полным» и «пустым», мельчайшими неделимыми атомами (ccrouoc) и пустым пространством, соответствует различию между «бытием» и «небытием» у Парменида. Сложность и изменчивость у Гераклита вытекала из различных перераспределений атомов. Пустое пространство считалось однородным и изотропным.
Атомы отличаются по форме ([joprprj), положению (Osaic) и различным конфигурациям (xaQi?) в материальных комбинациях. Для сравнения комбинации атомов сопоставляется последовательность букв в словах, и это привело к гипотезе, что атомистические идеи развивались только в цивилизациях с фонетическим алфавитом. Действительно, в Китае, где фонетического алфавита нет и его заменяют иероглифические знаки, идея частиц была неизвестна, а преобладала полевая и волновая концепции процессов в природе. Атомы Демокрита двигались по необходимости (avavxrj) в постоянном круговороте ((v.voc или Sivt)). Здесь, в противоположность позднейшим представлениям Аристотеля, движение означает только изменение положения в пустом пространстве. Все явления, все рождающееся и погибающее, возникают из слияния (аиухрюк;) и разделения (iy.axpiaic). Агрегатные состояния материи — газообразное, жидкое и твердое — объясняются разными плотностями атомов и их потенциальными возможностями к движению. С точки зрения современной кристаллографии, заслуживает внимания идея Демокрита о том, что даже атомы в твердых телах совершают колебания в пространстве.
Платон в диалоге «Тимей» предложил первую математическую модель атомизма. Изменения, смешивания и разделения элементов, о которых говорили досократики, были сведены к неизменным математическим закономерностям. В случае четырех элементов Эмпедокла, а именно огня, воздуха, воды и земли, классификация была под руками и непосредственно доступна восприятию. Еще Теэтет полностью опием все правильные многогранники, возможные в трехмерном (евклидовом) пространстве: тетраэдр, октаэдр, икосаэдр, куб и додекаэдр. Поэтому то, что предложил Платон, заключалось в сопоставлении четырех элементов Эмпедокла этим геометрическим строительным блокам.
Платон сознательно избегал использования для своих элементов демокритовского названия «атом», так как они могут быть разложены на отдельные плоские фигуры. Так, грани тетраэдров, октаэдров и икосаэдров представляют собой равносторонние треугольники, и если эти грани рассечь пополам, то получаются прямоугольные треугольники с длинами сторон 1, 2 и ч/З, в то время как квадратные грани кубов при рассечении пополам по диагонали образуют прямоугольные треугольники с длинами сторон 1, 1 и л/2. Как следствие, «жидкости» типа воды, воздуха и огня могут объединяться друг с другом, в то время как твердое тело, составленное из элементов земли, из-за разницы в треугольниках может превращаться только в другое твердое тело.
Затем Платон развивает нечто вроде физики элементарных частиц, в рамках которой отдельные элементы преобразуются друг в друга, а между «элементарными частицами» (т. е. соответствующими базовыми треугольниками) могут иметь место «обратимые явления» в соответствии с геометрическими законами. Например, преобразования элементов происходят в результате разрезания тел вдоль ребер. По Платону, такая возможность зависит от остроты углов в вершинах многогранников. С помощью более острых плоских углов при вершинах можно построить все правильные многогранники. Так, по порядку, каждый тетраэдр, куб, октаэдр и икосаэдр может в каждом случае создать не предыдущий в этом ряду или тот же самый, а только последующий многогранник. Вывод, следующий из этих рассуждений для философии природы, заключается в том, что огонь может разделить или растворить все элементы, земля — только воздух и воду, а воздух — только воду.
Платон решительно настаивал на том, что не все элементы имеют одинаковый размер. Например, чтобы объяснить, почему огонь может перевести воду из твердой формы в жидкую, он полагал, что в жидком состоянии элементы меньше и более подвижны, а в твердом состоянии они больше.
Избавление от огня называется охлаждением, а состояние после искоренения огня — отвердеванием. Огонь и воздух могут беспрепятственно проникать сквозь щели в строительных блоках из земли (кубах), не растворяя элементы земли. Сжатый воздух не может раствориться без разрушения элемента. Так, сжатие воздуха означает накопление октаэдров в самой идеальной из всех возможных конфигурации. Даже огонь не может, не разрушив октаэдров, проникнуть сквозь обязательно оставшиеся щели, плоские углы которых меньше, чем у всех элементов. В случае воды только огонь способен разрушить сильнейшую конденсацию. Щели между соседними икосаэдрами образуют плоские углы, которые не позволяют проникнуть туда ни земле, ни воздуху. Только огонь (тетраэдр) может проникнуть и растворить эту комбинацию.
На самом деле Платон развил внутренне согласованную математическую модель, позволявшую объяснить существование различных агрегатных состояний веществ и обратимых процессов, если только для интерпретации элементов принять его более или менее произвольные начальные условия. Естественно, что ряд следствий такой схемы для философии природы кажутся странными и забавными. Однако здесь мы имеем первую в истории науки попытку объяснить материю и ее состояния с помощью простых геометрических законов. Высшей точкой развития этих идей до сегодняшнего дня является современная теория элементарных частиц. Гей-зенберг по этому поводу сказал:
...Элементарные частицы имеют ту форму, которую им приписал Платон, так как это математически самая красивая и простая форма. Следовательно, корни всех явлений не в материи, а в математическом законе, симметрии, математической форме [2.8].
В Античности и Средних веках математический атомизм Платона находил мало поддержки. Для его последователей была очевидна основная проблема такой геометрической теории материи, ясно высказанная еще в диалоге «Тимей». Как можно объяснить функционирование живых организмов? Гипотеза о том, что определенные телесные формы имеют такой вид для того, чтобы исполнять определенные физиологические функции (так, глотка в форме воронки нужна для поглощения пищи), не может в общем случае быть выведена из теории правильных многогранников. Кроме того, сама идея объяснения изменяющихся и пульсирующих жизненных процессов с помощью «жестких» и «мертвых» геометрических фигур должна была казаться современникам Платона глубоко неестественной, спекулятивной и надуманной. Наши современники до сих пор затрудняются понять те окольные пути, которые выбирают научные объяснения, используя сложные и абстрактные математические теории. Именно здесь начинается философия природы Аристотеля.
Аристотель сформулировал свою концепцию баланса или «равновесия» в природе главным образом на основе того, как функционируют живые организмы — растения и животные. Течение жизненных процессов известно нам из повседневного опыта. Что может быть очевиднее, чем попытка сравнить и объяснить устройство остального, неизвестного и странного, мира через знакомые явления? Согласно Аристотелю, задача науки — объяснить принципы и назначение сложности и изменчивости в природе. Здесь Аристотель критиковал тех философов природы, которые отождествляли свои принципы с индивидуальными субстанциями. Отдельное растение или отдельное животное не являются простой суммой своих материальных строительных блоков. Аристотель называл то общее, которое придает отдельному сущему то, чем оно является, формой (ziboc,). То, что принимает форму, называется материей (иХг)). Но форма и материя не существуют сами по себе, а представляют принципы природы, выводимые из абстракций. Поэтому материя характеризуется также как потенция (Suvoqjic;) к обретению формы. Реальность (evEpyeia) наступает только после того, как материя обретает форму.
Наблюдаемые нами реальные живые существа подвергаются постоянным изменениям. В этом вопросе был прав Гераклит, а Парменид, для которого изменения были иллюзорны, ошибался. Изменения реальны. Но, согласно Аристотелю, Гераклит ошибался при сопоставлении изменений конкретной субстанции (огню). Аристотель объяснял такие изменения с помощью третьего, кроме материи и формы, принципа, а именно, недостатка формы (axepvm?), который восполнялся соответствующим изменением. Молодые растение или ребенок малы, слабы и недоразвиты. Они растут потому, что в соответствии с их естественными тенденциями (формой) подразумевается, что они станут большими, сильными и зрелыми. Отсюда делался вывод, что движение (xivsmc) в общем случае является изменением, переходом от возможности к реальности, «актуализацией потенции» (как сказали бы ученые Средних веков).
Задача физики — исследовать движение в природе в указанном всеобъемлющем смысле. Природа (сри-mq), в противоположность создаваемому человеком произведению искусства или техническому инструменту, понималась как все, что несет в себе самом принцип движения. Если аристотелевские понятия заставят нас, прежде всего, задуматься о тех жизненных процессах у растений, животных и людей, которые знакомы нам из повседневного жизненного опыта, то эти понятия покажутся нам весьма правдоподобными и удачными. Природа — это не каменоломня, из которой каждый может по своему желанию забирать отдельные куски. Сама природа представляется рациональным организмом, движения которого одновременно необходимы и целенаправленны. Аристотель различал несколько типов движения, а именно, количественное изменение за счет увеличения или уменьшения по величине, качественное изменение за счет изменения характеристик, и пространственное изменение за счет изменения местоположения. Аристотель выделял четыре проявления причинности, приводящей к изменениям. Почему растет растение? Оно растет, так как: 1) его материальные компоненты делают рост возможным (causa materi-alis); 2) его физиологические функции определяют рост (causa formalis)', 3) рост побуждается внешними обстоятельствами (питательными веществами в земле, водой, солнечным светом и пр.) (causa effoiens); 4) в соответствии с окончательной целью оно должно созреть и принять идеальную форму (causa finalis).
Затем Аристотель применил те же принципы, которые очевидным образом выводятся из рассмотрения жизненных циклов растений, животных и людей, к объяснению материи в более узком смысле, т. е. объяснению того, что позднее получило название неживой природы. Здесь Аристотель также исходил из непосредственного опыта. То, что мы наблюдаем, это не какое-то большое количество элементов, выступающих в качестве изолированных строительных блоков природы. На самом деле мы наблюдаем такие характеристики, как теплота и холод, влажность и сухость. Комбинации этих свойств приводят к следующим парам характеристик, определяющим элементы: теплый — сухой (огонь), теплый — влажный (воздух), холодный — влажный (вода), холодный — сухой (земля). Пары теплый — холодный и влажный — сухой как одновременные условия исключаются. Поэтому существуют только четыре элемента. Подобный вывод позднее критиковали как произвольный, но он демонстрирует метод Аристотеля, заключающийся в том, чтобы исходить не из абстрактных математических моделей, а непосредственно из чувственного опыта. Огонь, воздух, вода и земля в той или иной степени, с большей или меньшей интенсивностью, содержатся в реальных телах, которые вовлечены в постоянный круговорот превращений. Согласно Аристотелю, устранение холодности воды путем нагревания приводит к воздуху, а устранение влажности воздуха приводит к огню. Изменения в природе интерпретируются как процессы созревания и преобразования.
Каким образом такая, по преимуществу органическая, философия природы приводила к физическим объяснениям математической естественной науки, какой бы она ни была в то время? Были известны только два элементарных пространственных движения — по прямой линии и по окружности. Поэтому должны были существовать определенные элементы, для которых такие элементарные движения были естественными. Движения других тел определялись этими элементами и их естественными движениями и зависели от того, какое из этих движений преобладает в движении тела. Самым идеальным считалось движение по окружности, Только оно могло происходить бесконечно долго, поэтому такое движение было приписано неуничтожимому элементу. Это был пятый элемент (квинтэссенция), из которого были образованы неизменные небесные сферы и звезды. Непрерывные изменения в земном (подлунном) мире должны были противопоставляться неизменной регулярности, царящей в звездном (надлунном) мире. Процессы преобразований связывались с четырьмя элементами, для которых характерно прямолинейное движение, в частности, прямолинейное движение, направленное к центру мира, куда тяжелые элементы вода и земля стремятся, как к своему естественному местопребыванию, и прямолинейное движение к периферии лунной сферы, куда легкие элементы воздух и огонь устремляются, как к своему естественному местопребыванию.
К числу естественных движений относилось и свободное падение. Однако Аристотель пе поступил, как Галилей, и не начал с изучения изолированных движений в идеализированных экспериментальных ситуациях. Падающее тело наблюдалось в сложной окружающей среде без выделения сил трения («диссипативных» сил). В процессе свободного падения тело погружается в воздушной среде, как камень в воде. Таким образом, Аристотель представлял себе свободное падение как гидродинамический процесс, а не как ускорение тела в пустоте. Он предполагал постоянную скорость падения v, прямо пропорциональную весу тела р и обратно пропорциональную плотности среды d (например, воздуха). В современных обозначениях v ~ p/d. Это соотношение в то же время дало Аристотелю аргумент против пустоты атомистов. В вакууме с плотностью d — 0 все тела падали бы бесконечно быстро, чего, очевидно, не происходит.
Типичный пример вынужденного (вызванного человеком) движения — бросание тела, которое опять рассматривается в сложном окружении «диссипативных» сил. Согласно Аристотелю, неживое тело может двигаться только при наличии постоянной внешней причины движения. Представьте себе телегу на каменистой дороге в Древней Греции, которая немедленно останавливается, если осел (или раб) прекращают ее тянуть или толкать. Но почему брошенным камень продолжает двигаться после того, как рука отпускает его? Согласно Аристот елю, не может быть дейст вия на расстоянии в пустом пространстве (дальнодействия). Поэтому, говорит Аристотель, метатель передает движение непрерывной среде, окружающей камень, и эта среда проталкивает камень дальше. Аристотель полагает, что скорость v бросательного или толкательного движения пропорциональна приложенной силе К, т.е. v ~ К/р. Конечно, это не математические уравнения, связывающие измеримые величины, а всего лишь отношения пропорциональности качественных определяющих факторов, которые впервые возникли в такой алгебраической записи у средневековых физиков — последователей школы перипатетиков. Таким образом, в аристотелевской динамике, в отличие от динамики Галилея-Ньютона, каждое изменение положения (по прямой линии) требует причины движения (силы). Средневековая теория импетуса изменила динамику Аристотеля, приписав причину движения «импетусу» внутри брошенного тела, а не передаче движения со стороны внешней среды.
Каким образом динамика перипатетиков объясняет космические законы, управляющие небесами? Центральная симметрия космологической модели была основана на (не вызванном силами) круговом движении сфер, которое считалось естественным для «небесного» элемента, и на теории естественного местоположения (ло-куса) в центральной точке космоса. Однако Птолемей вычислил положение Земли на основе изотропии модели и используя силлогизм достаточного основания. Если дана полная эквивалентность всех направлений, то нет причины, по которой Земля должна двигаться в том или другом направлении.
Учитель Аристотеля — Платон — сформулировал центрально-симметричную модель движения небесных тел с Землей в центре. Вокруг нее все небо поворачивается по часовой стрелке вокруг небесной оси, проходящей через Землю. Солнце, Луна и планеты вращаются против часовой стрелки, находясь на поверхностях сфер с разным расстоянием до Земли, расположенных в последовательности: Луна, Меркурий, Венера, Солнце, Марс, Юпитер и Сатурн. Самая внешняя оболочка содержит сферу неподвижных звезд. Согласно представлениям Платона и Пифагора, периоды обращения связаны друг с другом целыми числами. У всех времен обращения существует общий множитель, так что по прошествии соответствующего времени все планеты вновь оказываются точно в том же месте. Движение каждой планеты порождает звук, так что все тоны движения сфер совместно образуют гармонию сфер в смысле упорядоченной музыкальной шкалы. Геометрические, арифметические и эстетические симметрии космоса звучат во Вселенной, как гармоничная музыка сфер. Вскоре в результате прямых наблюдений такая подчеркнуто симметричная модель космоса была поставлена под сомнение. Сложной проблемой стала нерегулярность орбит планет, особенно их попятные движения. Нерегулярности, наблюдающиеся на небе, вызывали беспокойство, особенно у философов пифагорейской школы, которые привыкли рассматривать небеса, в противоположность Земле, как царство вечной симметрии и гармонии.
С целью уменьшить сложность движений на небесах, Платон поставил знаменитый вопрос: с помощью каких регулярных, упорядоченных движений по окружности можно «спасти», т. е. кинематически объяснить планетные движения? Точная модель наблюдаемых орбит была получена после того, как Аполлоний из Пер-гама (~ 210 г. до н. э.) порекомендовал отказаться от общего центра всех сфер. Но при этом сохранялись круговая форма планетных движений и одинаковая скорость сфер. Согласно этому предложению, планеты равномерно вращаются но сферам (эпициклам), воображаемые центры которых равномерно движутся по большим окружностям (деферентам) вокруг центральной точки (Земли). Должным образом подбирая отношение скорости и диаметра двух круговых движений и варьируя их направление, можно было построить неожиданные формы орбит, которые нашли частичное применение в астрономии от Птолемея до Кеплера. При этом сохранялась сферическая симметрия отдельных моделей, даже если у них отсутствовал общий центр, а было много разных центров.
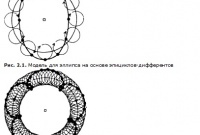
Следующие примеры применения техники эпициклов-деферентов показывают, какое множество кажущихся форм движения можно получить, подбирая соответствующим образом равномерные движения по окружности [2.9]. Таким образом, более понятными становятся взгляды платоновской философии о том, что за изменениями в явлениях стоят вечные и неизменные формы. На рис. 2.1 путем комбинации движений по деференту и эпициклу воспроизведена эллиптическая орбита. На рис. 2.2 показана замкнутая циклоида. Таким образом можно также представить меняющиеся расстояния между планетами и Землей. В принципе, можно воспроизвести даже угловые фигуры. Когда диаметр эпицикла достигает диаметра деферента, возникает строго прямая линия. С помощью подходящих комбинаций движения но эпициклам и деферентам можно получить даже правильные треугольники и прямоугольники, если изменить скорость движущейся с востока на запад планеты, которая сама движется но эпициклу, вращающемуся с запада на восток.
Если позволить небесному телу двигаться по второму эпициклу, центр которого движется по первому эпициклу, то можно получить множество эллиптических орбит, кривых, обладающих симметрией относительно отражений, а также непериодических и асимметричных кривых. С чисто математической и кинематической точек зрения задача Платона по «спасению явления» полностью решена. Поэтому, в принципе, платоновская редукция сложности в духе сведения к равномерному движению по окружности (модифицированная Аполлонием и Птолемеем) может до сих пор оказывать влияние на науку. В любом случае ее нельзя опровергнуть путем феноменологического описания кривых траекторий. В частности, с этой точки зрения, не только изменение ролей Земли и Солнца на противоположные в так называемой революции Коперника, но и переход Кеплера от круговых к эллиптическим орбитам представляются вторичными, так как обе инициативы можно свести к комбинации движений по окружности в согласии с техникой эпициклов-деферентов. Это ставит два вопроса:
1) Как можно математически обосновать это утверждение?
2) Если оно обосновано, то почему оно не играет роли в современных научных приложениях теории кривых?
Чтобы ответить на первый вопрос, следует обратиться к современной структуре аналитической геометрии. Но исторически Коперник и Кеплер тоже знали, каким образом используемые ими кривые (например, эллипсы) могут быть реконструированы с помощью техники эпициклов-деферентов.
Прежде всего, следует вспомнить, что точки на плоскости могут быть представлены комплексными числами z = х + iy = re'0 с соответствующими декартовыми координатами (ж, у) или полярными координатами (г, в). Сложение комплексных чисел соответствует тогда сложению векторов [2.10]. Равномерное движение точки по окружности с центром с, радиусом р и периодом Т можно представить в виде
z = c + xpeWM/T)+a) =
где переменная t соответствует времени, а параметр a — начальной фазе. Рассмотрим точку А, движущуюся согласно уравнению z = f(t). Пусть точка В движется относительно А по окружности радиусом р, периодом Т и начальной фазой а. Тогда движение точки В описывается уравнением
z = f(t)+pe(-",/T)+ia. (2)
Таким образом можно описать движение точки В по эпициклу, центр которого движется вокруг точки А. Добавление нового эпицикла математически описывается добавлением нового слагаемого „ вы.
ражение для г. Ясно, что
ресш/тщо = pe'«e(^u/T) = аеш
где а ф 0 — комплексное число, а к — действительное число. В случае обратного движения Т или к, соответственно, берутся отрицательными. Движение, возникающее в результате наложения п эпициклов, выражается уравнением
^ _ „ . „ Akvt | i ^ ikn! /o\
z — d\e +a>,e - + ... + a„e . (Л)
Рассмотрим сначала периодическое движение на плоскости z = /(/) (например, с периодом 2тг). Математически мы предполагаем, что / непрерывна и ограничена. Тогда функцию / можно представить в виде разложения в равномерно сходящийся ряд:
00
f(t) = J2 с"еШ- (4)
п=-оо
Отсюда можно строго математически доказать, что f(t) можно приблизить (аппроксимировать) суммами
N
s„(t)= J2 с«е"" О можно найти такой индекс Nit,
что для всех N 3- N„ и всех t выполняется 11 е раве 11 стш >
\№-sy(t)\ )
С астрономической точки зрения, это т результат означае т, ч то траектория периодического движения (с ограниченной вариацией) может быть аппроксимирована с любой степенью точности с помощью конечной суперпозиции движений по эпициклам.
Ясно, что до сих пор мы использовали только слагаемые с периодами эпициклов +2я\ ±7г, ±г,1г, iгтг, ... . Поэтому, в частности, использовались только соизмеримые периоды, которые можно, в духе пифагорейской традиции, выразить с: помощью отношений целых чисел. Но на самом деле непериодические кривые также можно аппроксимировать суперпозицией эпициклов, если допустить несоизмеримые периоды. Этот результат находит математическое обоснование в теореме Гарольда Бора о почти периодических функциях (1932) [2.1 1].
На второй вопрос, вопрос о том. почему для объяснения траекторий движения отвергнута техника эпициклов-деферентов, нельзя ответить, указав па наблюдение пропущенных в рамках этого подхода кривых. Математически наблюдаемые кривые, сколь бы экзотичными они ни были, могут быть в принципе объяснены (в рамках указанных выше очень широких математических ограничений) с помощью использовании в духе Платона и Аполлония древнем! стратегии сведения сложных движений к простым.
Однако в этом случае решающим вопросом является то, какие же движения совершают планеты «на самом деле», являются ли эти движения сложной комбинацией равномерных и ничем не вынуждаемых движений по окружности, которые с Земли кажутся эллиптическими траекториями.
или определенные силы на самом деле вынуждают планеты следовать по эллиптическим траекториям. Решение вопроса может быть найдено не геометрически или кинематически, а только динамически, т. е. с помощью соответствующей теории сил, следовательно, с помощью физики.
Помимо техники эпициклов-деферентов Птолемей использовал мнимые точки равновесия, относительно которых предполагалось, что планеты совершают равномерные движения по окружностям, кажущиеся неравномерными относительно Земли как центра. Эта техника оказалась полезной при вычислениях, но она утверждала нарушение центральной симметрии и поэтому сводилась к сделанному ad hoc предположению, мало приемлемому с точки зрения философии природы, как это специально отметил Коперник. Причины того, что Коперник поменял местами Землю и Солнце, были в основном кинематические. Действительно, на этом пути, обладающем большей симметрией, можно было достичь определенных кинематических упрощений. Так, в гелиоцентрической модели можно было интерпретировать кажущиеся обратные движения планет на небосводе как эффекты, обусловленные годовым движением Земли, которая, согласно Копернику, двигалась медленнее, чем внешние планеты - Марс, Юпитер и Сатурн, по быстрее, чем внутренние планеты — Венера и Меркурий. Но Коперник оставался глубоко консервативным философом, так как он рассматривал большую простоту в смысле «естественного» кругового движения как знак приближения к реальности.
При Иоганне Кеплере, первом великом математике современной астрономии. вера в просто ту оставалась неизменной. В мемуаре «Mysterium cos-mographicum» (1596) Кеплер вновь пытается обосновать расстояния в планетной системе с помощью правильных многогранников, попеременно вписанных в сферы и описанных вокруг них. Планеты Сатурн, Юпитер, Марс, Земля, Венера и Меркурий соответствуют шести сферам, вписанным одна в другую и разделенным в указанной последовательности кубом, тетраэдром, додекаэдром, икосаэдром и октаэдром. Конечно, умозрительные построения Кеплера нельзя было расширить так, чтобы учесть последующие открытия Урана, Нептуна и Плутона.
Однако Кеплер был уже в достаточной степени естествоиспытателем, чтобы не позволить себе надолго затеряться в платоновских догадках. Книга Кеплера «Astronomia nova» (1609) является уникальным документом, позволяющим шаг за шагом проследить постепенное исчезновение старой платоновской концепции простоты под постоянным давлением результатов точных измерений. В противоположность Копернику, Кеплер дополняет свои кинематические исследования оригинальными динамическими аргументами. Солнце уже не рассматривается по Кеплеру как лишенное физических функций тело в кинематически центральной точке, а считается динамической причиной движения планет. Таким образом, возникла новая задача математического определения этих сил. Кеплеровская динамическая интерпретация с помощью магнитных полей была лишь первой (ошибочной) попыткой. Успех пришел позже в теории тяготения Ньютона.
Простота звездного («надлунного») мира и сложность земного («подлунного») мира были часто встречающимися темами рассуждений в других культурах. Посмотрим на философию природы даосизма в древнем Китае. Откровенно говоря, эта философия окружена мифами и менее логично обоснована, чем греческая философия природы, а также требует больше интуиции и сопереживания. Тем не менее между двумя философиями существуют параллели. Даосизм описывает природу как большой организм, управляемый циклическими движениями и ритмами, такими как жизненные циклы поколений, династий и отдельных людей от рождения до смерти, пищевые цепочки, состоящие из растения, животного и человека, смена времен года, день и ночь, восход и заход звезд и т. п. Все связано со всем. За каждым следуют ритмы, как волны на воде.
Какие же силы являются первопричиной такой картины природы? Как и в учении Эмпедокла, в даосизме различаются две противоположные силы, называемые инь и ян, ритмическое увеличение и уменьшение которых управляет миром. В книге «Кей Ку Дзу» (IV в. до н. э.) говорится: «Ян периодически возвращается к первоначалу. Инь достигает максимума и прокладывает путь для ян» [2.12]. В то время как, согласно Аристотелю, все индивидуумы несут в себе свои естественные цели и движения, инь и ян в даосизме определяют внутренние ритмы отдельных личностей, энергия которых всегда возвращается к своим первоисточникам. Модель кругового вращения в даосизме позволяет объяснить создание календарей в астрономии, круговорот воды в метеорологии, пищевые цепочки и систему кровообращения в физиологии. Она черпает большую убедительность в жизненных ритмах природы, которые люди каждодневно ощущают и могут использовать для своего приспособления к жизни. Природа представляется целенаправленным организмом.
Примечательно, что в китайской философии природы отсутствуют понятия атомных частиц, и поэтому в ней не получила развития математическая механика в духе западного Возрождения. Вместо этого центральным пунктом является гармоничная модель природы с ритмичными волнами и полями, которые связуют все со всем. В рамках такой философии природы становятся понятными предпочтения, отдаваемые вопросам акустики, и ранние предрассудки, касающиеся явлений магнетизма и электростатики. Взгляды даосистов больше напоминают не взгляды Аристотеля, а философию природы стоиков. Все рассуждения стоиков сосредоточены на явлениях, развертывающихся в большом континууме и напоминающих волны на воде. Этот континуум у стоиков называется пневмой. Ее напряжения и колебания определяют различные состояния природы. Разнообразные формы природы являются всего лишь мимолетными картинами, возникающими за счет меняющихся натяжений пневмы. Конечно, современные рассуждения связывают это с картинами стоячих волн на воде, звуковыми волнами или картинами силовых линий магнитного поля. Тем не менее ни стоические, ни даосистские эвристические предпосылки не привели к созданию физической теории акустических явлений или магнитных полей, сравнимой с галилеевской механикой, основанной на атомистической философии природы. Возникновение порядка из сложных, нерегулярных и хаотичных состояний материи получило только качественное описание с помощью разных моделей Земли и неба.